조건부 이분산이라는 말은 금융시장에 임의의 이코노믹 쇼크가 가해졌을 때 그로 인한 변동성(분산)은 바로 직전 기에 영향을 받지만 시간이 지날수록 장기 평균 분산에 근접한다는 말이다. 이러한 현상을 모델링할 때 단일 변수 시계열의 경우에는 지난번 포스트 2020.10.20 - [시계열 모델링] - (G) ARCH 모형의 분석절차에서 살펴본 것처럼 비교적 간단하게 도출할 수 있다. 그러나 금융시장의 경우 서로 복잡하게 얽혀 있기 때문에 하나의 자산에 가해진 충격은 다른 자산 혹은 다른 나라의 금융시장에도 영향을 미치는 경우가 빈번하다.
상식적으로 생각해보자. 전일 다우지수가 박살이 났다. 적당히 박살 난 게 아니라 아주 그냥 아작이 났다고 치자. 다음날 코스피는??? 슬프지만 비슷할 확률이 매우 높다. 또한 실례로 IMF는 외환위기로 인하여 발생하였는데 환율이 급등(평가절하)을 하자 코스피는 어떠하였는가??? 돌아볼 필요도 없다. 자 만약 이분산을 고려하여 모델링을 하고자 한다면 위와 같은 현상을 고려한 다변량 이분산을 고려함이 바람직한데 이게 univariate 할 때와는 다르게 모델링하기가 쉽지 않다.
왜냐하면 다변량 분석의 경우 변수들 간의 공분산을 고려해야 하기 때문에 기존의 단일 변량 추정식에서 수행했던 평균, 조건부 이분산 방정식뿐만 아니라 조건부 공분산 방정식도 같이 모델링해야 한다. 또한 이로 인해 MLE를 이용하여 추정해야 하는 모수 역시 늘어난 인해 급증하게 된다. 그리고 우리를 힘들게 하는 것은 공분산 행렬이 항상 양정 부호를 가지는 것이 아니기 때문에(역행렬을 구하기 위한 행렬식을 풀 수 없는 현상 - ad-bc =0, 불능) 경우에 따라서 프로그램이 에러를 뛰우는 현상이 발생한다. (can't divide by zero... etc) 물론 이러한 현상은 초기값을 적절히 조절함으로써 해결할 수 있지만 경우에 따라서는 초기값을 전혀 알 수 없는 경우도 빈번하기에 녹록지 않다. 그러나 일정한 제약을 부여하는 방법으로 이러한 문제를 해결하는 모델이 등장했는데 바로 BEKK모형(Baba, Engle, Kraft and Kroner)인데 원리는 우선 평균 방정식을 OLS로 추정하여 회귀계수와 오 차 항 분산을 초기값으로 설정(모든 변수들에 대한 GARCH 추정치들의 제곱근을 초기값으로 설정)하여 반복적으로 계산하는 방법이다. 이 외 일정 상관관계(CCC : Constant Conditional Correlation) 모델, 가변 상수 모델(DCC :Dynamic Conditional Correlation), 단일 요인 GARCH 모델 등도 있으니 좀 더 상세한 내용을 알고 싶은 사람은 참고문헌을 살펴보자. [참고 : 금융시계열분석-김명직,장국현]
이론적 배경에 대해서는 이 정도로 살펴보고 언제나 그런 것처럼 실전분석으로 바로 돌입해보자. 아래의 코드는 S&P 500과 마이크로소프트의 이변량 GARCH 모형으로 모델링한 것이다. 코드의 원본은 깃허브(MGARCH, EWMA)에 있으니 참고하면 된다.
library(PerformanceAnalytics)
library(quantmod)
library(rugarch)
library(car)
library(FinTS)
library(rmgarch)
options(digits=4)
computer = "work"
if (computer == "home") {
setwd("")
}
if (computer == "work") {
setwd("")
}
#source("covEWMA.r")
# download data
symbol.vec = c("MSFT", "^GSPC")
getSymbols(symbol.vec, from ="2020-01-03", to = "2021-04-03")
colnames(MSFT)
start(MSFT)
end(MSFT)
# extract adjusted closing prices
MSFT = MSFT[, "MSFT.Adjusted", drop=F]
GSPC = GSPC[, "GSPC.Adjusted", drop=F]
# plot prices
plot(MSFT)
plot(GSPC)
# calculate log-returns for GARCH analysis
MSFT.ret = CalculateReturns(MSFT, method="log")
GSPC.ret = CalculateReturns(GSPC, method="log")
# remove first NA observation
MSFT.ret = MSFT.ret[-1,]
GSPC.ret = GSPC.ret[-1,]
colnames(MSFT.ret) ="MSFT"
colnames(GSPC.ret) = "GSPC"
# create combined data series
MSFT.GSPC.ret = merge(MSFT.ret,GSPC.ret)
# plot returns
plot(MSFT.ret)
plot(GSPC.ret)
# scatterplot of returns
plot( coredata(GSPC.ret), coredata(MSFT.ret), xlab="GSPC", ylab="MSFT",
type="p", pch=16, lwd=2, col="blue")
abline(h=0,v=0)
#
# compute rolling correlations
#
# chart.RollingCorrelation(MSFT.ret, GSPC.ret, width=20)
cor.fun = function(x){
cor(x)[1,2]
}
cov.fun = function(x){
cov(x)[1,2]
}
roll.cov = rollapply(as.zoo(MSFT.GSPC.ret), FUN=cov.fun, width=20,
by.column=FALSE, align="right")
roll.cor = rollapply(as.zoo(MSFT.GSPC.ret), FUN=cor.fun, width=100,
by.column=FALSE, align="right")
par(mfrow=c(2,1))
plot(roll.cov, main="20-day rolling covariances", ylab="covariance", lwd=2, col="blue")
grid()
abline(h=cov(MSFT.GSPC.ret)[1,2], lwd=2, col="red")
plot(roll.cor, main="100-day rolling correlations",ylab="correlation", lwd=2, col="blue")
grid()
abline(h=cor(MSFT.GSPC.ret)[1,2], lwd=2, col="red")
par(mfrow=c(1,1))
#' Compute RiskMetrics-type EWMA Covariance Matrix
#'
#' Compute time series of RiskMetrics-type EWMA covariance matrices of returns.
#' Initial covariance matrix is assumed to be the unconditional covariance
#' matrix.
#'
#' The EWMA covariance matrix at time \code{t} is compute as \cr \code{Sigma(t)
#' = lambda*Sigma(t-1) + (1-lambda)*R(t)t(R(t))} \cr where \code{R(t)} is the
#' \code{K x 1} vector of returns at time \code{t}.
#'
#' @param factors \code{T x K} data.frame containing asset returns, where
#' \code{T} is the number of time periods and \code{K} is the number of assets.
#' @param lambda Scalar exponential decay factor. Must lie between between 0
#' and 1.
#' @param return.cor Logical, if TRUE then return EWMA correlation matrices.
#' @return \code{T x K x K} array giving the time series of EWMA covariance
#' matrices if \code{return.cor=FALSE} and EWMA correlation matrices if
#' \code{return.cor=TRUE}.
#' @author Eric Zivot and Yi-An Chen.
#' @references Zivot, E. and J. Wang (2006), \emph{Modeling Financial Time
#' Series with S-PLUS, Second Edition}, Springer-Verlag.
#' @examples
#'
#' # compute time vaying covariance of factors.
#' data(managers.df)
#' factors = managers.df[,(7:9)]
#' cov.f.ewma <- covEWMA(factors)
#' cov.f.ewma[120,,]
#'
covEWMA <-
function(factors, lambda=0.96, return.cor=FALSE) {
## Inputs:
## factors N x K numerical factors data. data is class data.frame
## N is the time length and K is the number of the factors.
## lambda scalar. exponetial decay factor between 0 and 1.
## return.cor Logical, if TRUE then return EWMA correlation matrices
## Output:
## cov.f.ewma array. dimension is N x K x K.
## comments:
## 1. add optional argument cov.start to specify initial covariance matrix
## 2. allow data input to be data class to be any rectangular data object
if (is.data.frame(factors)){
factor.names = colnames(factors)
t.factor = nrow(factors)
k.factor = ncol(factors)
factors = as.matrix(factors)
t.names = rownames(factors)
} else {
stop("factor data should be saved in data.frame class.")
}
if (lambda>=1 || lambda <= 0){
stop("exponential decay value lambda should be between 0 and 1.")
} else {
cov.f.ewma = array(,c(t.factor,k.factor,k.factor))
cov.f = var(factors) # unconditional variance as EWMA at time = 0
FF = (factors[1,]- mean(factors)) %*% t(factors[1,]- mean(factors))
cov.f.ewma[1,,] = (1-lambda)*FF + lambda*cov.f
for (i in 2:t.factor) {
FF = (factors[i,]- mean(factors)) %*% t(factors[i,]- mean(factors))
cov.f.ewma[i,,] = (1-lambda)*FF + lambda*cov.f.ewma[(i-1),,]
}
}
# 9/15/11: add dimnames to array
dimnames(cov.f.ewma) = list(t.names, factor.names, factor.names)
if(return.cor) {
cor.f.ewma = cov.f.ewma
for (i in 1:dim(cor.f.ewma)[1]) {
cor.f.ewma[i, , ] = cov2cor(cov.f.ewma[i, ,])
}
return(cor.f.ewma)
} else{
return(cov.f.ewma)
}
}
#
# calculate EWMA covariances and correlations
#
lambda <- 0.94
cov.ewma <- covEWMA(as.data.frame(MSFT.GSPC.ret), lambda=lambda)
## 2. extract conditional variance and correlation
### conditional variance
MSFT.GSPC.cond.cov <- cov.ewma[,2,1];
### conditional correlation
t <- length(cov.ewma[,1,1]);
MSFT.GSPC.cond.cor<- rep(0,t);
for (i in 1:t) {
MSFT.GSPC.cond.cor[i]<- cov2cor(cov.ewma[i,,])[1,2];
}
### Plots
par(mfrow=c(2,1))
plot(x=time(as.zoo(MSFT.GSPC.ret)), y=MSFT.GSPC.cond.cov,
type="l", xlab="Time", ylab="Covariance", lwd=2, col="blue",
main="EWMA Covariance between MSFT and S&P500");
grid()
abline(h=cov(MSFT.GSPC.ret)[1,2], lwd=2, col="red")
plot(x=time(as.zoo(MSFT.GSPC.ret)), y=MSFT.GSPC.cond.cor,
type="l", xlab="Time", ylab="Correlation", lwd=2, col="blue",
main="EWMA Correlation between MSFT and S&P500");
grid()
abline(h=cor(MSFT.GSPC.ret)[1,2], lwd=2, col="red")
par(mfrow=c(1,1))
# compute rolling covariances and correlations using longer window
roll.cov = rollapply(as.zoo(MSFT.GSPC.ret), FUN=cov.fun, width=252,
by.column=FALSE, align="right")
roll.cor = rollapply(as.zoo(MSFT.GSPC.ret), FUN=cor.fun, width=252,
by.column=FALSE, align="right")
par(mfrow=c(2,1))
plot(roll.cov, main="252-day rolling covariances",
ylab="covariance", lwd=2, col="blue")
grid()
abline(h=cov(MSFT.GSPC.ret)[1,2], lwd=2, col="red")
plot(roll.cor, main="252-day rolling correlations",
ylab="correlation", lwd=2, col="blue")
grid()
abline(h=cor(MSFT.GSPC.ret)[1,2], lwd=2, col="red")
par(mfrow=c(1,1))
# compute EWMA covariances and correlations using longer half-life
half.life = 125
lambda = exp(log(0.5)/half.life)
cov.ewma <- covEWMA(MSFT.GSPC.ret, lambda=lambda)
## 2. extract conditional variance and correlation
### conditional variance
MSFT.GSPC.cond.cov <- cov.ewma[,2,1]
### conditional correlation
t <- length(cov.ewma[,1,1])
MSFT.GSPC.cond.cor<- rep(0,t)
for (i in 1:t) {
MSFT.GSPC.cond.cor[i]<- cov2cor(cov.ewma[i,,])[1,2]
}
### Plots
par(mfrow=c(2,1))
plot(x=time(as.zoo(MSFT.GSPC.ret)), y=MSFT.GSPC.cond.cov,
type="l", xlab="Time", ylab="Covariance", lwd=2, col="blue",
main="EWMA Covariance between MSFT and S&P500")
grid()
abline(h=cov(MSFT.GSPC.ret)[1,2], lwd=2, col="red")
plot(x=time(as.zoo(MSFT.GSPC.ret)), y=MSFT.GSPC.cond.cor,
type="l", xlab="Time", ylab="Correlation", lwd=2, col="blue",
main="EWMA Correlation between MSFT and S&P500")
grid()
abline(h=cor(MSFT.GSPC.ret)[1,2], lwd=2, col="red")
par(mfrow=c(1,1))
#
# DCC estimation
#
# univariate normal GARCH(1,1) for each series
garch11.spec = ugarchspec(mean.model = list(armaOrder = c(0,0)),
variance.model = list(garchOrder = c(1,1),
model = "sGARCH"),
distribution.model = "norm")
# dcc specification - GARCH(1,1) for conditional correlations
dcc.garch11.spec = dccspec(uspec = multispec( replicate(2, garch11.spec) ),
dccOrder = c(1,1),
distribution = "mvnorm")
dcc.garch11.spec
dcc.fit = dccfit(dcc.garch11.spec, data = MSFT.GSPC.ret)
class(dcc.fit)
summary(dcc.fit)
slotNames(dcc.fit)
names(dcc.fit@mfit)
names(dcc.fit@model)
# many extractor functions - see help on DCCfit object
# coef, likelihood, rshape, rskew, fitted, sigma,
# residuals, plot, infocriteria, rcor, rcov
# show, nisurface
# show dcc fit
dcc.fit
# plot method
plot(dcc.fit)
# Make a plot selection (or 0 to exit):
#
# 1: Conditional Mean (vs Realized Returns)
# 2: Conditional Sigma (vs Realized Absolute Returns)
# 3: Conditional Covariance
# 4: Conditional Correlation
# 5: EW Portfolio Plot with conditional density VaR limits
# conditional sd of each series
plot(dcc.fit, which=2)
# conditional correlation
plot(dcc.fit, which=4)
# extracting correlation series
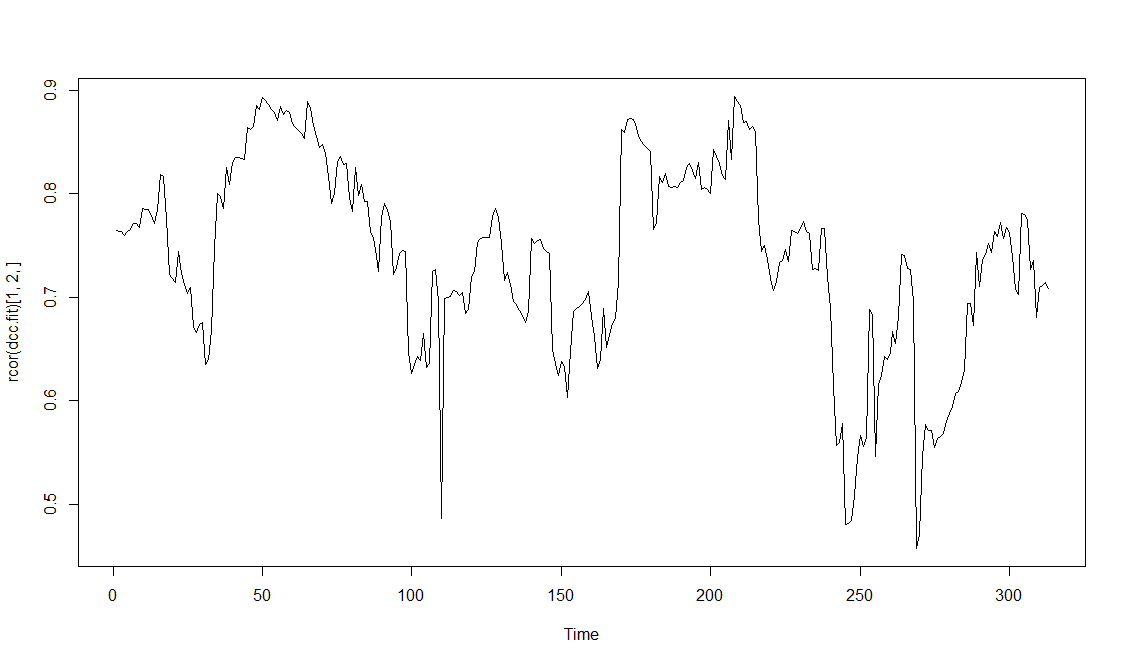
ts.plot(rcor(dcc.fit)[1,2,])
#
# forecasting conditional volatility and correlations
#
dcc.fcst = dccforecast(dcc.fit, n.ahead=100)
class(dcc.fcst)
slotNames(dcc.fcst)
class(dcc.fcst@mforecast)
names(dcc.fcst@mforecast)
# many method functions - see help on DCCforecast class
# rshape, rskew, fitted, sigma, plot, rcor, rcov, show
# show forecasts
dcc.fcst
# plot forecasts
plot(dcc.fcst)
죽 드래그해서 집어넣고 코드를 돌려보면 아래와 같이 에센 피 지수와 마이크로소프트 주식 간의 time varing cor 그래프를 살펴볼 수 있는데 위에서 설명한 CCC 모형에 비해 시간 가변 한 상관관계를 확인할 수 있다. 마찬가지로 다른 지수 혹은 주식과의 관계에 대해서도 종목코드(MSFT, GSPC,,, etc)만 변경하면 돌려볼 수 있다. 코스피 지수와 종목도 퀀트모드에서 제공하기는 하지만 해외주식처럼 시계열로 제공하지는 않는 것 같고 당일의 종가에 한해서만 가져올 수 있다. 뭐가 그리 대단한 자료라고 자꾸 숨기는지 모르겠는데 별 그지 같아도 룰이 그러니 어쩔 수 있나. 위 코드에서 데이터는 지난번 포스트에서 다룬 엑셀로 차트 데이터 가져오기로 대체하면 별다른 문제없이 돌아갈 것이라 본다. 2020.08.28 - [증권사 API] - 이베스트 증권 차트 TR 만들어보기(VBA 활용 - 업종 차트 편)
'시계열모델링' 카테고리의 다른 글
| VAR(Vector Auto Regressive Model) 모델을 이용한 주가 예측 (0) | 2022.07.18 |
|---|---|
| 국면전환(Regime-Switching)모형을 이용한 코스피추세 예측 (0) | 2021.08.20 |
| 다이나믹 모델링 : 칼만필터(Kalman Filter)를 이용한 주가예측 (2) | 2021.06.28 |
| 확률 미분방정식(SDE)을 이용한 주가 시뮬레이션 (0) | 2021.06.22 |
| 파마 프렌치의 3요인 모형 (0) | 2020.12.14 |




댓글