일반적으로 미분방정식이라 함은 한 개 또는 그 이상의 종속변수를 한 개 혹은 그 이상의 독립변수에 대한 도함수를 포함하는 방정식을 의미하며 이때 하나의 독립변수를 포함하는 방정식을 상미분 방정식이(ordinary differential equation)라 하고 이를 푸는 방법은 변수분리, 적분인자 등의 해석적 방법과 오일러, 룬게-쿠타 방법 등의 수치적으로 풀이할 수도 있다. 그런데 1개 이상의 독립변수가 확률과정을 가지는 재미난 현상을 모델링하기 위해 등장한 것이 바로 확률 미분 방정식(SDE : stochastic differential equation)이다.
예를 들어 쇠구슬을 3층에서 떨어뜨렸을 때 일정 시간 뒤에 물체의 낙하지점은 중력가속도를 이용한 미분방정식으로 풀 수 있고 수 차례의 반복실험에서도 같은(실험에 의한 오차는 있을 수 있지만) 결과를 얻을 수 있다. 바로 이렇게 산출된 방정식은 결정론적 모형이라고 한다.
그러나 비커에 물을 한 컵 채워놓고 거기에 꽃가루를 뿌리면 이 가루의 움직임은 위의 현상처럼 간단하게 구해지지가 않는다. 바로 물 분자의 우연한 변동에 의해 매번의 실험마다 서로 다른 결과값을 보이게 된다. 이렇게 애매한 운동을 모델링하기 위해 나온 것이 바로 확률론적 모형기법이고 대표적인 것이 브라운 운동(Brownian motion)인데 1827년 스코틀랜드 식물학자 로버트 브라운(Robert Brown)이 발견한, 액체나 기체 속에서 미소입자들이 불규칙하게 운동하는 현상이다. [위키백과]
그런데 이러한 브라운 운동은 수학적으로 매우 복잡할 뿐만 아니라 미분불가능하다. 다만 몇 가지 규칙에 의해 스칼라 및 벡터에 따른 이토 과정(위너 과정의 이토 적분으로 정의되는 확률 과정이다.[위키백과])을 통해 모수적 확률 미분방정식을 구할 수 있다. [참고 :R프로그램에 기반한 미분방정식의 이해 이재길 저 | 황소걸음 아카데미]
일반적인 확률 미분방정식의 확률과정은 아래와 같이 표현할 수 있는데(https://en.wikipedia.org/wiki/Stochastic_differential_equation)

위 식을 해석함에 있어 한 가지 주의할 점은 아주 짧은 시간 사이에 확률과정 Xt의 변화는 기대값은 mu(xt,t), 분산은 sigma(x,t)^2 의 정규분포를 따르고 과거의 움직임과는 독립이라는 점이다. mu는 드리프트, sigma는 확산계수라 하며 이 방정식을 풀어서 얻어지는 확률적 과정 Xt는 통상 미래의 값은 과거가 아닌 현재의 값에 영향을 받는 마르코프적 성격을 가지고 있다. 그놈의 마르코프과정은 여러 군데 자주 등장하는데 지난번 포스트(2020.11.18 - [텐서플로우] - 강화학습으로 주식투자하기 - 이론적 배경)에서도 다루었으니 참고하면 좋을 듯 하다.
도대체 이딴게 퀀트(알고리즘 기반의 투자)와 무슨 연관이 있을까? 자 늘 그래왔듯이 실전으로 돌입해보자. 실전에서는 확률 미분방정식을 비교적 쉬운 방법으로 패키지만 설치하면 구현할 수 있는 R 을 이용할 예정이고 아래의 코드와 같이 패키지 yuima 를 이용해서 쉽게 풀어낼 수 있다.
#install.packages("yuima")
library(yuima)
#GBM(기하학적 브라운운동) : 주식 가격의 변동이 평균이 mu, 분산이 sigma 를 따른다고 가정.
#주식시장의 드리프트텀(확률적 추세)은 무위험이자율이고 나머지는 변동성이라고 가정.
#그렇다. 적어도 이 이론에 따르면 주식투자를 하면 은행금리만큼은 먹을 수 있다.
#그런데 왜 내가 사면 내리고 내가 팔면 오를까하는 사람들은 우연적 변동에 자꾸 털려서 그렇다.
#x나게 잘하던가 그것도 아니면 x나게 버티던가. 가지가지 하지말고 하나만 해라. 그러면 결국 길이 보일 것이니.
mu<-0.01 #무위험이자율 1%
sigma<-0.2 #삼성전자의 연평균 변동성 약 20%(일 표준편차를 구하고 *sqrt(250) 하면 대략 비슷하게 구해짐.)
stock<-80200
stockModel=setModel(drift="mu*s",diffusion = "sigma*s",state.variable = "s",
time.variable = "t",solve.variable = "s",xinit = stock) #앞으로 3년치 주가를 시뮬레이션하고 구간은 1일로 한다.(365*3~1000)
stocksample<-setSampling(Terminal = 3, n=1000)
output<-setYuima(model=stockModel,sampling = stocksample)
stocksimul<-simulate(output,true.parameter = list(mu=mu,sigma=sigma))
plot(stocksimul)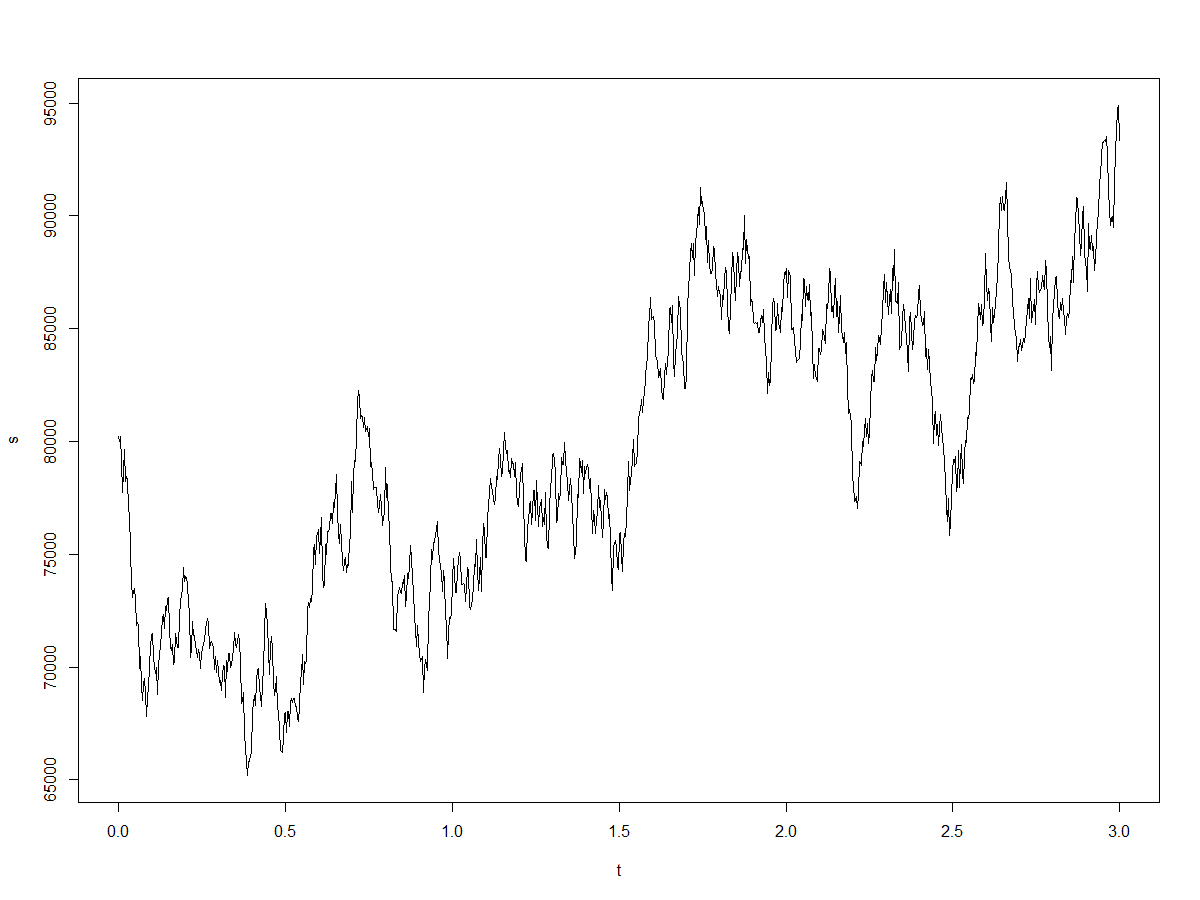
그렇다. 굉장히 어려운 과정을 겪어서 몬테카를로를 수행했지만 이건 돌릴 때마다 다르다. 우연변동의 시뮬레이션이니까 그럴 수 밖에 없다. 그렇다면 이걸 왜 할까? 믿을 수도 없는데. 물론 무수히 많은 시뮬레이션 중의 하나인 어떠한 임의의 결과값을 그대로 받아들이기는 어렵다. 자 그러면 역으로 이제는 실제 히스토리컬 데이터를 이용하여 삼성전자의 과거 대수(log)차분의 분포를 한번 그려보자.
#작업경로를 지정하는 명령어
setwd("")
df<-read.csv("samsung_elect.csv",
header=TRUE, na.strings = "")
lndf<-diff(log(df$y))
plot(lndf)
hist(lndf)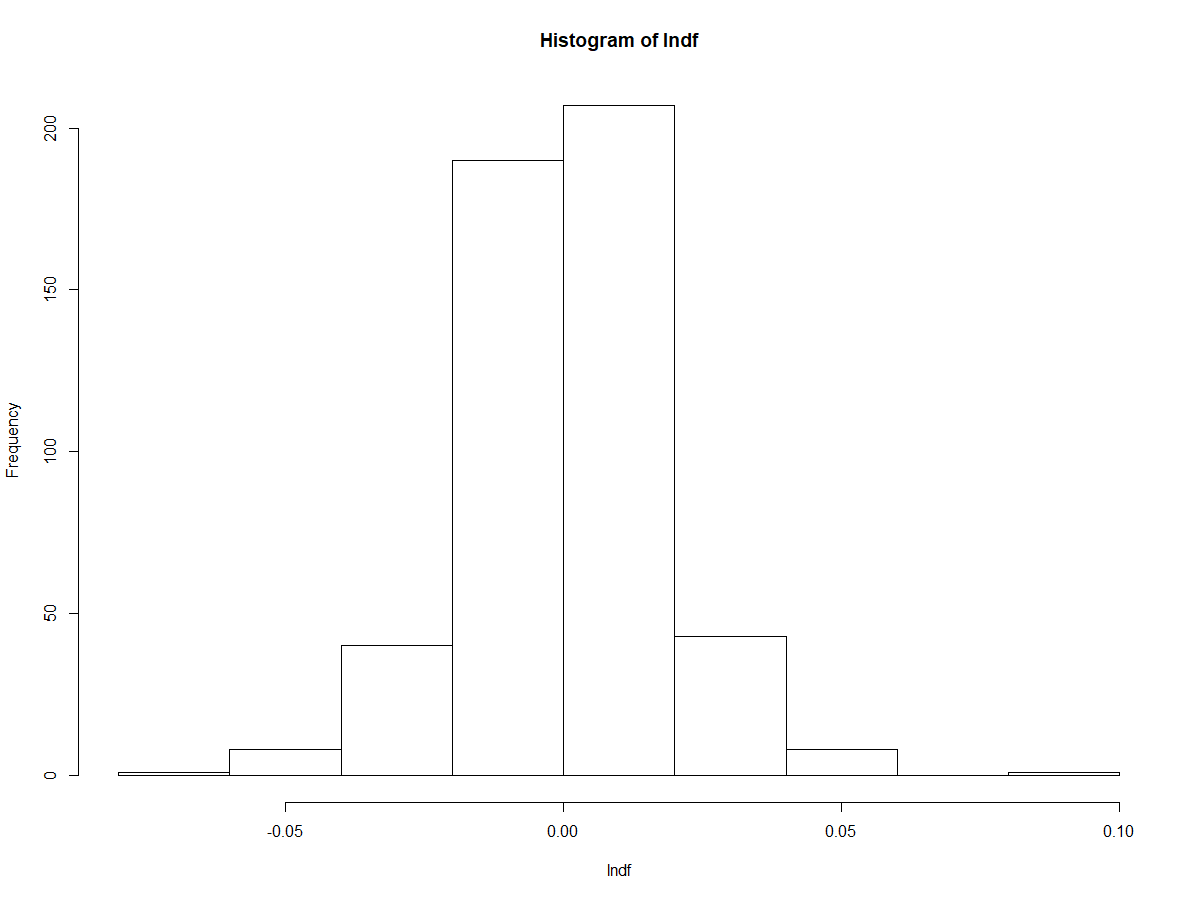
어라? 이거 어디서 많이 본거 같은데 라는 생각이 들 것이다.가우시안 분포[ 1/(2*pi*sigma^2)*exp{-(x-mu)^2/2} ]를 굉장히 많이 닮았다. 물론 정규분포에 대한 검증까지는 해보지 않았지만 단순히 과거 500거래일의 분포만 살펴보았는데도 어느 정도 유추는 가능하다. 당시의 경제상황, 글로벌 정세 등에 따라 위너프로세스의 움직임은 매번 다를 수 있지만 돌이켜 보면 정규분포 하더라까지는 성립할 수 있을 것이다. (금융시계열의 경우 비이성적과열로 인한 fat-tail이 자주 관측되기는 하지만 너무 디테일하게는 말고..)
바로 이런 점을 이용해서 블랙-숄즈, 머턴은 GBM을 이용하여 시장이 최소한 주식과 같은 최소한 하나의 위험자산과 단기금융, 현금, 채권과 같은 하나의 안전자산으로 구성되어 있다고 가정한 뒤 자산에 관해서는 다음과 같이 정의하여 옵션가격 결정모형을 유도해내고 당연히 그렇듯 노벨상도 탔다.
- (안전자산) 안전자산의 수익률은 변화가 없다 그러므로 '무위험 수익률'이라고 부른다.
- (랜덤워크) 주식가격의 순간 로그 수익률은 무한한 임의보행이다. 더 자세히 말하자면 기하학적 브라운 운동을 따른다. [위키백과]
다음 포스트에서는 머턴모델을 R의 sde 패키지를 이용해 유도해보도록 하자.
종목분석 전용 생성형AI 무엇이든 물어보세요
https://leenaissance.site/
리네상스 테크놀로지
인공지능 주식대장, 무엇이든 물어보세요.
leenaissance.site
'시계열모델링' 카테고리의 다른 글
| Multivariate GARCH(다변량 이분산 모형) (0) | 2021.08.19 |
|---|---|
| 다이나믹 모델링 : 칼만필터(Kalman Filter)를 이용한 주가예측 (2) | 2021.06.28 |
| 파마 프렌치의 3요인 모형 (0) | 2020.12.14 |
| Facebook prophet(예언자)을 이용한 주가예측 모델링 (0) | 2020.12.02 |
| (G)ARCH 모형의 분석절차 (0) | 2020.10.20 |




댓글