자본 자산 가격 결정 모델 (CAPM)로 알려진 전통적인 모델은 주식의 수익률과 시장 전체 수익률을 설명하는데 하나의 변수만 사용한다. 반대로 Fama–French 모델은 세 가지 변수를 사용하는데 파마과 프렌치는 기존 CAPM 에 두 가지 요소를 추가했다.
Capital asset pricing model - Wikipedia
In finance, the capital asset pricing model (CAPM) is a model used to determine a theoretically appropriate required rate of return of an asset, to make decisions about adding assets to a well-diversified portfolio. The model takes into account the asset's
en.wikipedia.org
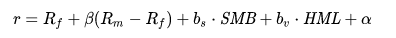
여기서 r은 포트폴리오의 기대 수익률, Rf 는 무위험 수익률, Rm 은 시장 포트폴리오의 수익률입니다. "세 요소" β 는 기존 β와 유사 하지만 일부 작업을 수행 할 두 개의 추가 요소가 있으므로 같지는 않다. 위 식에서 SMB 는 " Small [시가 총액] Minus Big"를 의미하고 HML 은 " High [book-to-market ratio] Minus Low"를 의미한다.
이러한 요소는 시총 순위 (BtM 순위, Cap 순위) 및 사용 가능한 과거 시장 데이터로 구성된 포트폴리오의 조합으로 계산되며 Kenneth French의 웹 페이지 에서 과거데이터를 확인할 수 있다 . 또한 SMB 및 HML이 정의되면 해당 계수 bs 및 bv 는 선형 회귀에 의해 결정되며 양수 값뿐만 아니라 음수 값도 사용할 수 있다. (위키백과-원문)
우선 위의 분석을 수행하기 위해서는 무위험이자율, 벤치마크지수(코스피/코스닥), 시가총액, PBR 에 대한 시계열 자료가 필요하다. 첨부되어 있는 Excel 파일은 지난 포스트(2020/08/28 - [증권사 API/이베스트] - 이베스트증권 차트TR 만들어보기(VBA 활용 - 주식차트편))외 업종차트 등을 참고하면 충분히 가공이 가능하니 직접 해봐도 좋고 이것 저것 귀찮은 사람은 첨부파일을 다운로드해서 활용해도 좋다.
첨부된 엑셀파일을 열어보면 분석대상 유니버스는 지난번 포스트 2020/11/12 - [데이터마이닝 with R/실전머신러닝] - 의사결정나무를 이용해서 HTS 조건검색식 만들어보기 에서 다뤘던 조건검색을 이용한 종목군들을 대상으로 하였고 요약정보에는 투자유니버스 100종목에 대한 시가총액, PBR자료, 변수정보는 2가지 가공을 거쳐서 무위험이자율, 코스닥지수, 주가수익률(신신제약), 파마-프렌치의 SMB, HML을 분석 변수에 담았다. 단 여기서 무위험이자율은 KODEX 국고채3년물(인버스)의 가격 데이터를 이용하여 산출하였다. 왜 인버스인가 물어보면 곤란하다. 금리가 오르면 채권가격이 떨어지기 때문에 금리의 수익률을 추정하기 위해서는 반대로 움직이는 기초자산을 선택하거나 아니면 아예 금리자체를 변수로 활용해야 한다.
자 이제부터 위 공식대로 데이터를 가공한 뒤 R의 lm 함수를 사용하여 중회귀를 돌려보자. 대략적으로 식은 신신제약 ~ 상수항 + 베타*체계적 위험 + 시총요인 + 저평가 요인 정도가 될 것이다. 모형설정이 완료되었으니 이제는 아래의 코드를 참고해서 실전 분석을 돌려보자.
#작업경로를 지정하는 명령어
setwd("")
#데이터 끌어오기(중회귀자료, 다수의 독립변수와 하나의 종속변수)
mydatat<-read.csv("fama.csv",
header=TRUE, na.strings = "")
#벤치마크수익률과 무위험이자율의 차이.
systematic<-mydatat$dkosdaq - mydatat$drf
#개별주식의 수익률과 무위험이자율의 차이.
nonsystematic<-mydatat$dstock - mydatat$drf
#파마-프렌치의 2가지 추가요인.
SMB<-mydatat$SMB
HML<-mydatat$HML
model <- lm( "nonsystematic ~ systematic + SMB + HML" , data = mydatat)
summary(model)
predicted <- model$coefficients[1]+model$coefficients[2] * systematic +
model$coefficients[3]*SMB +model$coefficients[4]*HML
plot(predicted, mydatat$dstock, xlab = "추정위험리워드."
,ylab = "관측위험리워드.",main = "파마프렌치:신신제약")
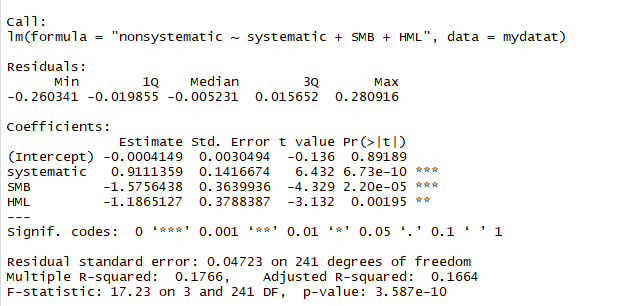
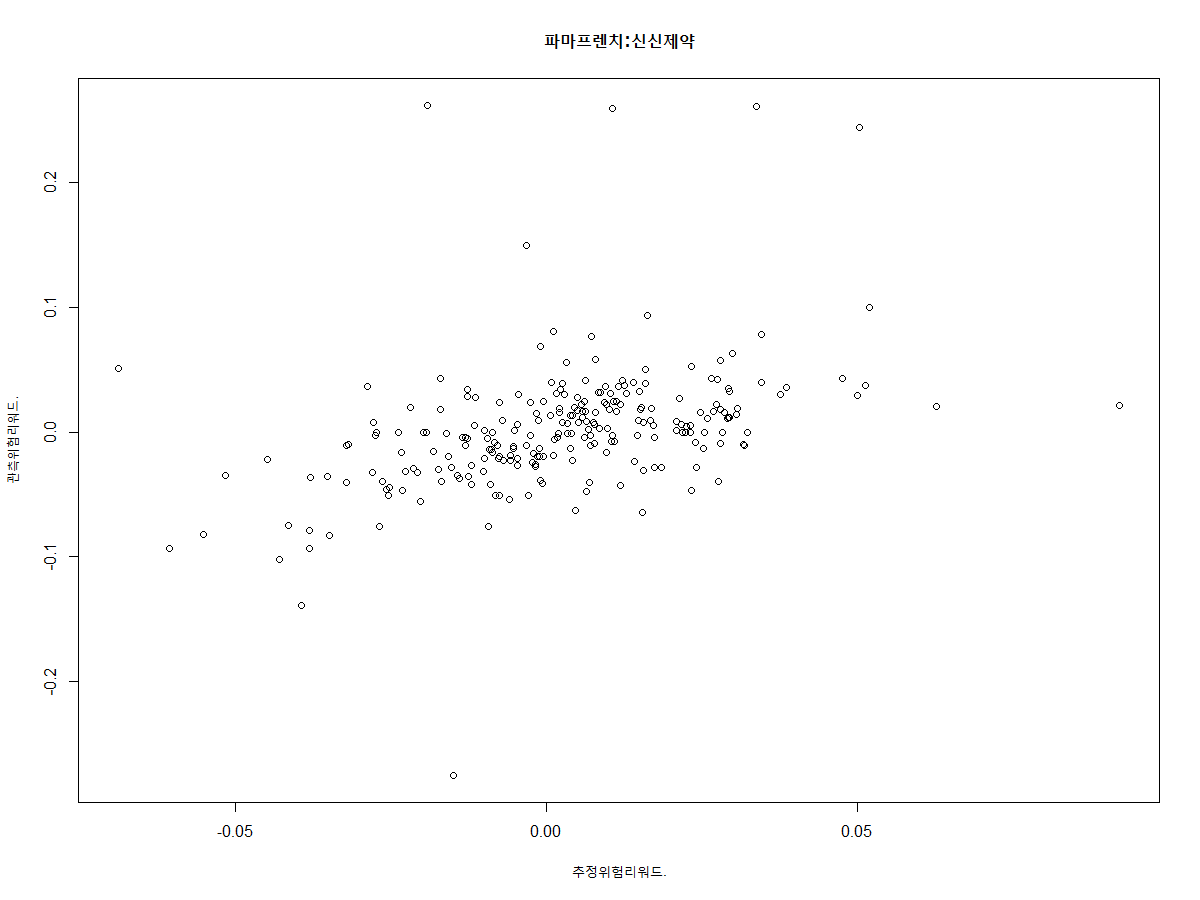
분석 후 요약정보를 살펴보면 신신제약의 경우 시스템리스크와 SMB, HML 모두 유의미한 것으로 분석되었지만 세가지 요인들이 프리미엄의 분산을 설명하는 정도(R^2)는 겨우 16% 정도 밖에 되지 않는 것으로 나온다. 이는 아래의 위험보상에 관한 그래프와 같이 양 극단값이 많이 존재하는 것을 봐도 알 수 있다. 다시 말해 신신제약의 경우에는 3가지 요인 외에 중요한 다른 무언가가 포함되어 있다는 뜻이 된다.
다만 위의 결과를 해석함에 있어서 유의성의 정도에 따라 중요성을 판단해보자면 신신제약은 시장의 영향을 가장 많이 받는다(systematic 변수의 유의성이 가장 신뢰도가 높음) 정도가 될 것이다. 물론 위 유니버스 종목 100개 중에는 꽤 유의미한 결과를 보이는 종목도 있을 수 있으니 시간이 될 때 다 돌려봐야겠다.
주식전용 생성형 인공지능, 무엇이든 물어보세요.
https://leenaissance.site/
리네상스 테크놀로지
인공지능 주식대장, 무엇이든 물어보세요.
leenaissance.site
'시계열모델링' 카테고리의 다른 글
| 다이나믹 모델링 : 칼만필터(Kalman Filter)를 이용한 주가예측 (2) | 2021.06.28 |
|---|---|
| 확률 미분방정식(SDE)을 이용한 주가 시뮬레이션 (0) | 2021.06.22 |
| Facebook prophet(예언자)을 이용한 주가예측 모델링 (0) | 2020.12.02 |
| (G)ARCH 모형의 분석절차 (0) | 2020.10.20 |
| ARIMA 모형의 분석절차(확률적 모형분석) (0) | 2020.10.19 |




댓글