동분산의 가정은 고전적 최소자승법에서 횡단면 자료의 오차분산이 일정하다는 가정을 중요시하여 시계열 자료의 분석에서도 모든 t에 대해 분산이 일정하다는 안정성 조건을 중요시였기 때문에 ARMA 모형에서는 잔차의 분산이 동일하다고 가정한다. 하지만 실제 시계열 자료 특히 금융시계열에서는 무작위적으로 일정한 구간을 벗어난 극단값이 관측되는 경우가 많다. 이러한 오류가 자주 발생을 하자 시간의 흐름에 따라 변화하는 분산에 대한 연구로 ARCH, GARCH 모형이 개발되었다.
이러한 시계열 자료의 특징은 변동성의 군집화 현상을 보이는데 높은 변동성을 가진 구간이 그렇지 않은 구간에 비해서 집중되어 있고 분포를 살펴보면 fat-tail을 가진 뾰족한 분포를 가지는 것이 특징이다. 그래서 로버트 앵글은 특정시점 t기의 오차의 분산은 과거의 t-1기 오차항의 제곱에 의해 설명할 수 있다고 가정하고 오차항의 분산은 과거 오차항의 제곱 값에 의존하여 시간의 경과에 따라 변화하는 이분산적인 특징을 갖는다고 가정, 평균방정식(arima, regression)과 분산방정식(arch)에 대해 동시적인 추정하는 ARCH 모형을 개발하게 된다.
그러나 ARCH(p) 모형을 추정함에 있어 p의 차수가 커지게 되면 추정화하는데 상당한 어려움(계산의 복잡성)이 존재할 수 있다. 따라서 분산방정식에 분산항의 시차변수를 포함시키는 방법으로 슬레브에 의해 일반화된 자기회귀 조건부 이분산 모델 GARCH(p,q)이 등장하게 되었다.
ARCH, GARCH 모두 시간에 따라 가변적인 조건부 분산을 다룬다는 점에서 동일하고 분산이 장기적으로 평균회귀한다는 가정은 동일하지만 ARCH의 경우 추정치가 수렴하지 않을 경우도 있고 변동성의 자기회귀계수가 (-)음수인 경우도 발생할 수 있다. 또한 GARCH 모형의 경우 모델의 특성상 긍정적인 쇼크와 부정적인 쇼크에 대한 비대칭적 효과에 대해서도 모델링이 가능하다는 점에서 한 단계 업그레이드 된 모델이라 할 수 있다.
그렇다면 이제부터 일반적인 (G)ARCH의 분석절차를 알아보자.
1. (G)ARCH 효과의 존재 여부 검정 : 2020/10/19 - [머신러닝 with R/시계열모델링 with R] - ARIMA 모형의 분석절차(확률적 모형분석)을 통해 이미 잔차에 이분산이 존재함을 알아냈다. 이번 포스트에서는 아래의 2번 부터 수행을 해보자.
2. (G)ARCH 추정 및 평가 : 수리적 모델링에 대해서는 관련서적을 참고하고 이 포스트에서는 실전 R코드 분석을 바로수행한다. 첫 번째 추천도서는 수리적 모델링 및 R코드 위주의 예제 실습에 용이하고 아래의 금융시계열 분석은 수리적 모델링 및 eviews, gauss 코드 위주의 예제 실습에 용이하다.
 |
|
 |
|
3. 예측 및 해석
#작업경로를 지정하는 명령어
setwd("")
mydatat<-read.csv("jisu.csv",
header=TRUE, na.strings = "")
#--------(G)ARCH 추정 및 평가.------------
o=mydatat$코스피지수
#로그차분을 수행.
do<-diff(log(o))
library(fGarch)
#일반적인 arma 모형.
ga<-garchFit(~arma(3,1),do)
#Ljung-Box Test : 잔차와 잔차의 제곱에 대한 자기상관이 존재함.
summary(ga)
#arma + arch 모형.
gac<-garchFit(~arma(3,1)+garch(1,0),do)
#Ljung-Box Test : 잔차와 잔차의 제곱에 대한 자기상관이 존재함.
summary(gac)
#arma + garch 모형.,
gag<-garchFit(~arma(3,1)+garch(1,1),do)
#Ljung-Box Test : 잔차와 잔차의 제곱에 대한 자기상관 없음.
summary(gag)
#--------(G)ARCH 예측.------------
#일반적인 arma 모형.
gfa<-forecast::forecast(ga@fitted,h=4)
forecast::accuracy(gfa)
#arma + arch 모형.
gfc<-forecast::forecast(gac@fitted,h=4)
forecast::accuracy(gfc)
#arma + garch 모형.,
#RMSE에서 유의미한 차이가 있음.
gfg<-forecast::forecast(gag@fitted,h=4)
forecast::accuracy(gfg)
#예측오차의 비교를 통해서도 귀무가설을 기각-> 유의미한 차이가 있음.
forecast::dm.test(gfa$residuals,gfg$residuals)
forecast::dm.test(gfc$residuals,gfg$residuals)
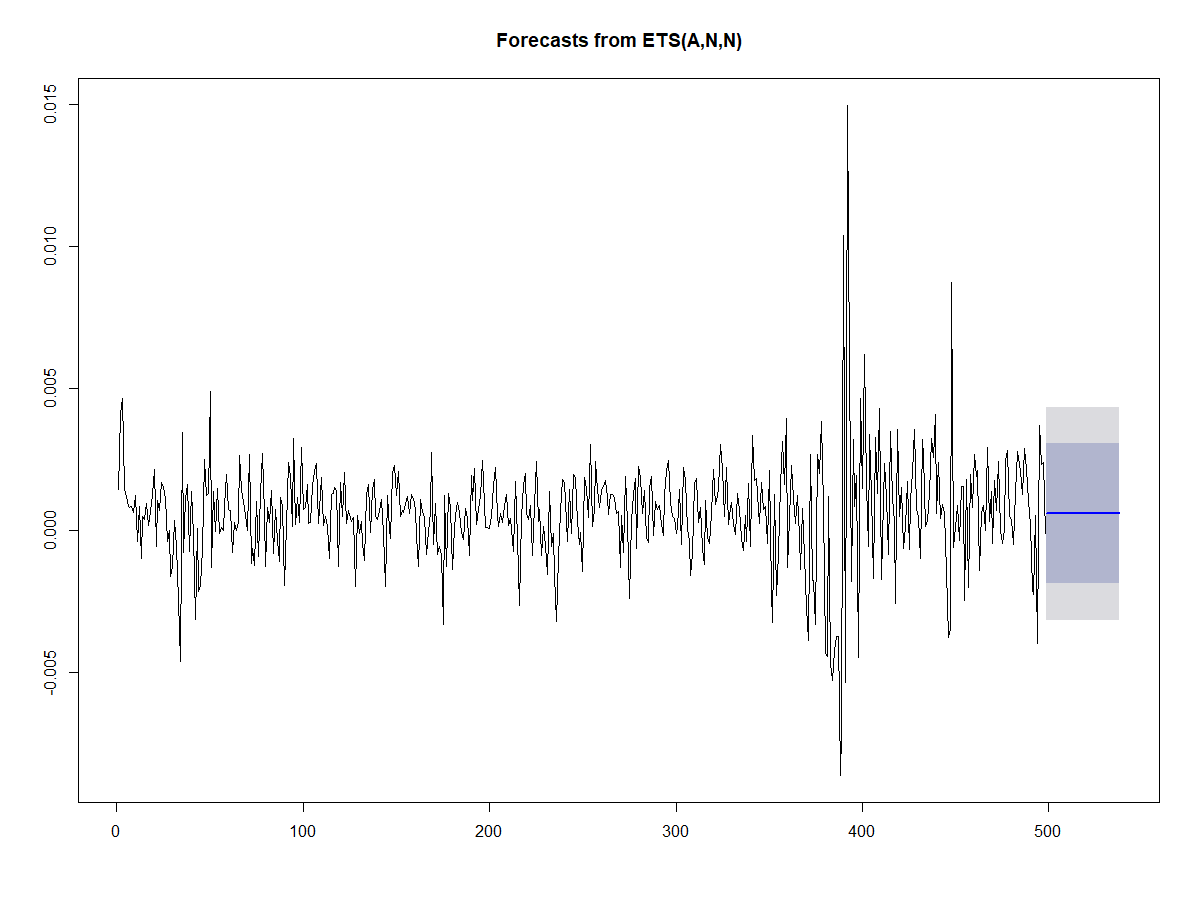
분석의 결과 arma, arma+arch 모형의 검정통계량(Ljung-Box)에서는 잔차 및 잔차의 제곱에 대한 자기상관이 존재하는 것으로 분석되었고 garch 에서는 유의미한 자기상관이 존재하지 않는 것으로 분석되었다. 또한 이렇게 분석한 모델을 통한 예측성능 평가에서도 garch 로 추정한 모델과 그렇지 않은 모델사이에 유의미한 차이가 존재하는 것으로 분석되었고 RMSE 평가지표에서 우수한 성능을 보이고 있다. 다만 자크베라, 샤피로 분석에서는 잔차의 정규성이 존재하지 않는다고 나오는데 조금 더 대표본일 경우에는 이러한 문제가 해결될 것이라 판단된다.
'시계열모델링' 카테고리의 다른 글
| 파마 프렌치의 3요인 모형 (0) | 2020.12.14 |
|---|---|
| Facebook prophet(예언자)을 이용한 주가예측 모델링 (0) | 2020.12.02 |
| ARIMA 모형의 분석절차(확률적 모형분석) (0) | 2020.10.19 |
| 시계열 자료의 분해법 (0) | 2020.10.19 |
| 시계열 자료의 평활법 - 회귀평활 part 2 (0) | 2020.10.19 |




댓글