의사결정트리에 관한 이론적 배경은 지난번 포스트(2020/09/10 - [데이터마이닝 with R/인과관계분석 with R] - 의사결정나무(Decision Tree) with R)를 참고하면 되는데 그래도 다시 한번 간략히 복습하고 넘어가자. 트리를 만드는 과정은 재귀적 분할이라고도 하는데 임의의 데이터를 부분 집합으로 나누고 그 다음은 더 작은 부분집합으로 반복적으로 분할하다 보면 나누어진 집단의 속성이 매우 동질적이어서 더 이상 부분으로 나누기 힘든 구간까지 반복하는 방법을 의미한다.
지난번 포스트에서 rpart를 이용한 트리모형을 구현했다면 이번 포스트에서는 C5.0 엔진을 이용해 볼 예정인데 rpart 에 비해 우수한 점은 수치나 명목에 대해서 특별히 가리지 않고 중요하지 않은 속성치는 알아서 제거해주는 고도화된 엔진이다. 학습의 원리는 비교적 간단한 엔트로피 기반의 알고리즘을 이용하며 여기서 엔트로피란 쪼개어진 부분집합의 순도를 표현한다. 단, 여기서 말하는 순도는 우리가 금이나 귀금속처럼 순도 99%가 더 좋다라고 판단하면 곤란하다. 여기서는 약간 다른 개념이라는 점만 짚고 넘어가자.
여기서 엔트로피는 무질서도를 의미한다. 예를 들어 [1]로 구성된 단일 숫자 집합에서 얻을 수 있는 정보는 매우 정적인데 반해 [1,13,52,,,3432,33,,,] 등에서 얻을 수 있는 정보의 종류는 평균은? 분산은? 짝수의 집합인가? 소수의 집합인가? 기타 등 등..매우 많다. 그렇다면 2번째 집합을 동일한 속성을 가진 부분집합으로 쪼개다 보면 나누어진 부분집합들의 엔트로피는 점점 작아지게 된다. 마찬가지로 C5.0엔진은 엔트로피를 최소화하는 분기점을 찾아내고 부분 집합의 동질성을 최대화하는 방법론을 선택하였다.
그 다음으로 살펴볼 방법은 규칙기반의 분류모형이다. 이는 엔트로피와는 조금 다르게 명제를 통해서 결과를 검증하는 과정을 반복한다. 예를 들어 ROA가 1이상인 종목들은 BUY 일 것이다라는 첫 번째 규칙을 설정하고 분류를 진행하면 도중에 ROA가 10이상인 종목들에 대해서 HOLD 가 나올 경우 ROA는 1과 10 사이에 존재해야 BUY일 것이다와 같은 새로운 규칙을 추가하게 된다. 그런데 ROA가 1미만인 종목들에 대해서도 BUY라는 결과를 만나게 되면 이번에는 PER가 10이상인 종목들 중 ROA가 1미만이면 BUY라는 새로운 규칙을 생성해나가게 된다.
이렇게 데이터에 적합하도록 새로운 규칙들을 생성하여 데이터의 부분들을 커버해나가다 보면 더 이상 커버안되는 부분이 없을 때까지 반복을 하고 최종적인 규칙을 도출하게 된다. 다만 이러한 방법들은 매우 많은 시행착오를 필요로 하기에 속도가 너무 느리다는 단점이 있고 불규칙성이 심한 데이터가 많이 포함될 경우 모델의 신뢰도가 현저히 떨어지는 오류가 있었다. 바로 이러한 단점을 해결하기 위해 새롭게 등장한 모형이 있는데 그게 ripper 모델이다. 원리는 IREP(incremental reduced error pruning)을 채택하여 단점을 많이 개선했다. 좀 더 상세한 자료를 원하는 사람은 직접 관련서적을 참고하길 바란다.
 |
|
자 지금부터 실전으로 돌입하자. 우선 첨부된 엑셀파일을 그래도 이용해도 좋고 직접 가공하길 원하는 사람은 이전 포스트(2020/11/09 - [증권사 API] - 특정기업의 FNG 요약, 마켓컨센서스 가져오기)를 참고해서 만들어도 좋다. 엑셀을 적절한 위치에 다운 받은 뒤 아래의 코드를 수행해보자. 중간 중간 주석을 첨부했으니 참고하길 바란다. 단 여기에서 말하는 변수 V1=PER, V2=PBR, V3=ROA, V4=ROE, V5=EVEBITDA이다. 데이터에 네이밍을 했으면 좀 더 보기 수월할 건데 아래에는 구현하지 않았으니 직접해보길 바란다(names...)
#install.packages("RWeka")
library(readxl)
#작업경로를 지정하는 명령어
setwd("")
mydatae<-read_excel("fng.xlsx",
sheet='fng',
col_names=TRUE,
na = "NA")
#-----------------데이터 가공----------------
#총 데이터 중 매수와 관망의 수..
opinion<-table(mydatae$최종)
#매수와 관망의 비중 분석.
round(prop.table(opinion)*100, digits=2)
#훈련데이터를 만들기위한 재무비율값
analysis<-cbind(mydatae$PER,mydatae$PRB,mydatae$ROA,mydatae$ROE,mydatae$EVEBIT)
#라벨링을 해주기 위한 단계
mydatae$최종<-factor(mydatae$최종)
str(mydatae$최종)
#적절한 단계로 잘라준다.
a_train<-as.data.frame(analysis[1:320,])
a_test<-as.data.frame(analysis[321:369,])
r_train<-mydatae$최종[1:320]
r_test<-mydatae$최종[321:369]
#-----------------C50엔진을 이용한 분류----------------
#install.packages("C50")
library(C50)
tree_model<-C5.0(a_train,r_train)
#roa는 -3.52초과.이고 pbr은 0.35초과.인 종목들에 대해 BUY.
summary(tree_model)
tree_predict<-predict(tree_model,a_test)
library(gmodels)
#비교결과 HOLD인 종목들에 대해서 BUY라고 분석한 종목들이 꽤 있지만
#정답레이블 자체를 5개 분석기관의 만장일치제로 선택했기 때문에
#오답률이 높다고만은 볼 수 없다.
CrossTable(x=r_test,y=tree_predict,prop.chisq = FALSE)
#C5모델은 패널티를 부여하여 오류의 유형에 따른 비용을 고려할 수 있다.
matrix_op<-list(c("BUY","HOLD"),c("BUY","HOLD"))
names(matrix_op)<-c("fcst","real")
matrix_cost<-matrix(c(0,0,2,0),2,2,dimnames = matrix_op)
tree_model_cost<-C5.0(a_train,r_train,costs = matrix_cost, trials = 10)
#roa는 -1.34초과.이고 pbr은 0.35초과.인 종목들에 대해 BUY.
#roa는 상동이며 pbr이 0.35이하인 종목일 경우 per가 70.78 초과인 종목들에 대해 BUY.
summary(tree_model_cost)
tree_predict_cost<-predict(tree_model_cost,a_test)
#패널티를 부여한 결과 HOLD 사인에 BUY를 하는 경우의 수가 1 줄어들었다.
#드라마틱하지는 않은 결과이지만 여하튼 패널티가 정상적으로 먹힌 것 같다.
#여기서 패널티를 3이상으로 주게되면 정답과 거의 동일한 패턴을 보이는데
#이렇게 할 경우 너무 과적합의 우려가 있다.
CrossTable(x=r_test,y=tree_predict_cost,prop.chisq = FALSE)
#-----------------rpart를 이용한 분류----------------
library(rpart)
rt=rpart(r_train~.,data=a_train, method="class")
#roa는 -1.3이상이고 pbr은 0.35이상인 종목들 중
#evebitda가 12.88이상 40.36미만.인 종목들에 대해서 BUY
summary(rt)
plot(rt,branch = 0.5, margin = 0.05)
text(rt,use.n = T, all = T, cex=0.9)
#-----------------Rweka를 이용한 분류----------------
library(RWeka)
rip_model<-JRip(r_train~.,data=a_train)
summary(rip_model)
#roe<=2.1 and ev<=11.48 and per<=26.39 --> HOLD
#ev>=50.56 -->HOLD
#위의 조건에 부합되지 않으면 BUY.
#요약하면 roe>2.1, 11.48<ev<50.56, per>26.39 를 만족하는 종목군이 BUY의 의견이 높음.


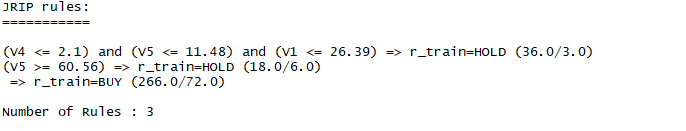
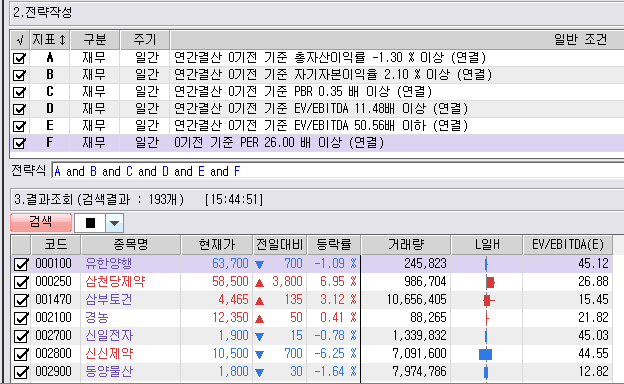

결과들을 모두 종합(단순하게 공통된 조건을 합산)해보면 [ROA > -1.3, ROE > 2.1, PBR > 0.35, 11.48<EV<50.56, PER > 26] 라는 결과가 나오고 이러한 조건식을 증권사에서 제공하고 있는 조건검색기에 입력하면 아래의 그림과 같이 약 193개의 종목군이 나온다. 물론 이것만 가지고 포트폴리오를 구성하기에는 다소 무리가 있다. 20 종목 이상을 살거면 그냥 인덱스펀드에 가입하면 된다. 그러나 이러한 종목군들을 투자유니버스의 대상으로 삼고 2차적인 특징, 모멘텀(시계열 분석)을 이용해서 투자의사 결정에 반영한다면 꽤나 의미있는 분석이 될 수 있을 것이다.
이베스트증권의 HTS에서는 나의 조건식에 대한 과거 데이터를 기준으로 성과검증을 수행해 볼 수 있으니 테스트해보면 썩 나쁘지는 않은 것으로 나온다. 물론 시장이 좋았기 때문에 이걸 종목선정의 효과라고 보기에는 다소 무리가 있을 수 있다는 점 고려해야 한다.
위에서 분석된 조건식을 만족하는 종목들에 대해 GRU 신경망으로 매수와 매도 의견에 관한 프로그램을 MFC C++을 이용하여 만들어봤다. 쿠폰번호만 댓글신청 후 발급받으면 사용에 제약이 없기 때문에 직접 코딩이 어려운 사람은 아래의 링크를 참고하면 다운로드가 가능하다.
'실전머신러닝' 카테고리의 다른 글
| 인공지능이 파헤친 세력의 숨겨진 패턴, 파이썬 강화학습으로 마스터하는 세력주 공략법! (0) | 2024.04.21 |
|---|---|
| 인공지능을 활용한 최적화된 MACD지표로 수익성을 강화하고 스마트하게 투자하기! (0) | 2024.04.18 |
| KNN, 나이브베이즈 분류를 이용해서 종목분석하기 (0) | 2020.11.10 |
| 머신러닝 개요 with R (0) | 2020.11.06 |
| Keras 를 이용한 텍스트마이닝으로 뉴스예측하기 with Python (0) | 2020.09.17 |




댓글